E3 – Intensités et tensions
Sujet 1⚓︎
Ex1⚓︎
1. Ajouter le sens du courant sur le circuit ci-dessous :
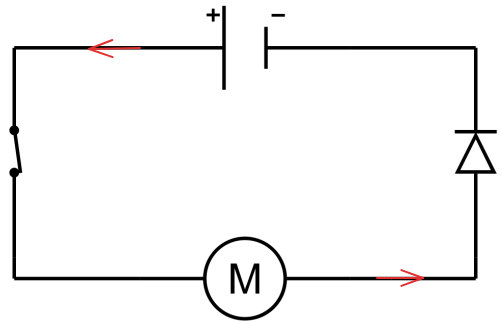
2. Cite la loi d'unicité de l'intensité qui s'applique au circuit ci-dessus.
On applique la loi d'unicité de l'intensité dans un circuit en série. L'intensité est constante dans un circuit en série..
3. Cite et explique la loi des tensions qui s'applique au circuit ci-dessus.
On applique la loi d'additivité des tensions dans un circuit en série. La tension aux bornes du générateur est égale à l'addition des tensions aux bornes des autres dipôles. On applique ici la relation \(U_G=U_M+U_L\) car on considère que la tension aux bornes d'un interrupteur fermé est de 0V.
4. L'intensité qui sort de la pile est notée I₁ et vaut 350 mA. Combien vaut l'intensité qui entre dans le moteur que l'on note I₂ ? Justifie.
On est dans un circuit en série, on utilise la loi d'unicité de l'intensité. L'intensité étant constante, on a I₁ = I₂ = 350 mA..
5. On mesure la tension aux bornes de plusieurs dipôles, on obtient alors :
• Pour la pile : \(U_G = 12,0 V\).
• Pour la diode : \(U_D = 5,0 V\).
Quelle est la valeur de la tension \(U_M\) aux bornes du moteur ?
On applique la loi d'additivité des tensions dans un circuit en série. On applique ici la relation \(U_G=U_M+U_D\) ce qui donne \(12,0=U_M+5,0\). On a donc \(U_M=12-5=7V\), la tension aux bornes du moteur est de 7,0V.
Ex2⚓︎
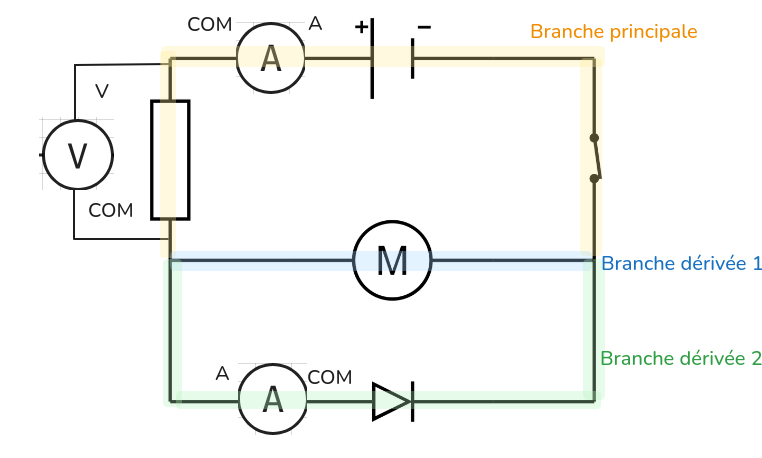
Ajoute sur le schéma :
□ un ampèremètre dans la branche principale.
□ un ampèremètre dans une branche dérivée.
□ un voltmètre pour mesurer la tension aux bornes de la résistance.
Ex3⚓︎
On mesure dans le circuit ci-dessous les intensités \(I_2 = 250 mA\) et \(I = 650 mA\).
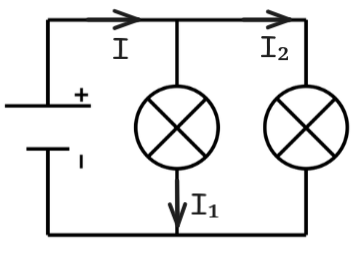
En justifiant à l'aide d'une loi et d'un calcul, donner la valeur de l'intensité \(I_1\).
On est dans un circuit en dérivation on utilise donc la loi d'additivité des intensités : l'intensité de la branche principale (I) est égale à l'addition des autres intensités. On a donc : \(I = I_1 + I_2\).
Soit : \(650 = I_1 + 250\) donc \(I_1 = 650 - 250 = 400 mA\).
Bonus : Si l'intensité I₁ vaut 2,0 A et l'intensité I₂ vaut 650 mA, combien vaudrait l'intensité I ?
On applique la même loi avec 650 mA = 0,65 A. Donc : \(I=2,0 + 0,65 = 2,65A\).
Sujet 2⚓︎
Ex1⚓︎
1. Ajouter le sens du courant sur le circuit ci-dessous :
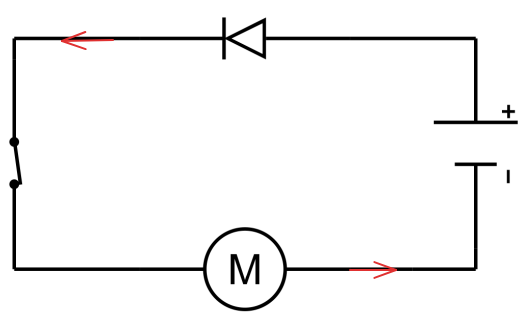
2. Cite la loi d'unicité de l'intensité qui s'applique au circuit ci-dessus.
On applique la loi d'unicité de l'intensité dans un circuit en série. L'intensité est constante dans un circuit en série..
3. Cite et explique la loi des tensions qui s'applique au circuit ci-dessus.
On applique la loi d'additivité des tensions dans un circuit en série. La tension aux bornes du générateur est égale à l'addition des tensions aux bornes des autres dipôles. On applique ici la relation \(U_G=U_M+U_D\) car on considère que la tension aux bornes d'un interrupteur fermé est de 0V.
4. L'intensité qui sort de la pile est notée I₁ et vaut 250 mA. Combien vaut l'intensité qui entre dans le moteur que l'on note I₂ ? Justifie.
On est dans un circuit en série, on utilise la loi d'unicité de l'intensité. L'intensité étant constante, on a I₁ = I₂ = 250 mA..
5. On mesure la tension aux bornes de plusieurs dipôles, on obtient alors :
• Pour la pile : \(U_G = 12,0 V\).
• Pour la diode : \(U_D = 7,0 V\).
Quelle est la valeur de la tension \(U_M\) aux bornes du moteur ?
On applique la loi d'additivité des tensions dans un circuit en série. On applique ici la relation \(U_G=U_M+U_D\) ce qui donne \(12,0=U_M+7,0\). On a donc \(U_M=12-7=5V\), la tension aux bornes du moteur est de 5,0V.
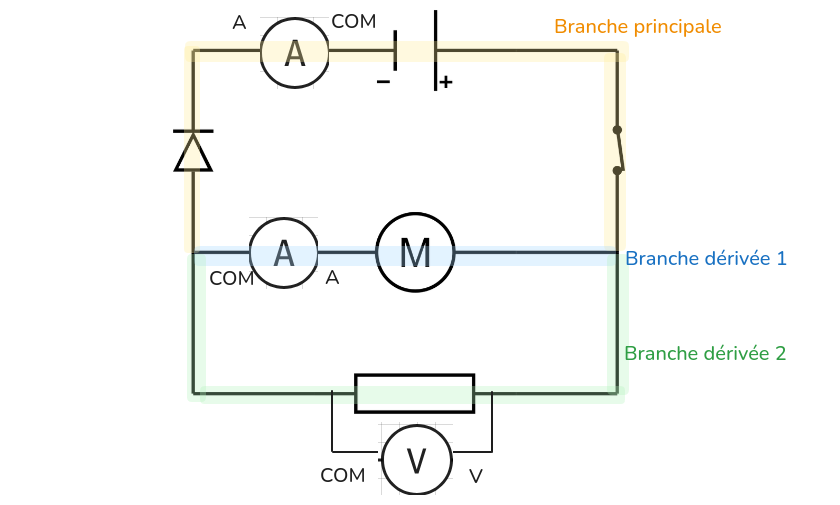
Ex2⚓︎
Ajoute sur le schéma :
□ un ampèremètre dans la branche principale.
□ un ampèremètre dans une branche dérivée.
□ un voltmètre pour mesurer la tension aux bornes de la résistance.
Ex3⚓︎
On mesure dans le circuit ci-dessous les intensités \(I_2 = 250 mA\) et \(I_3 = 550 mA\).
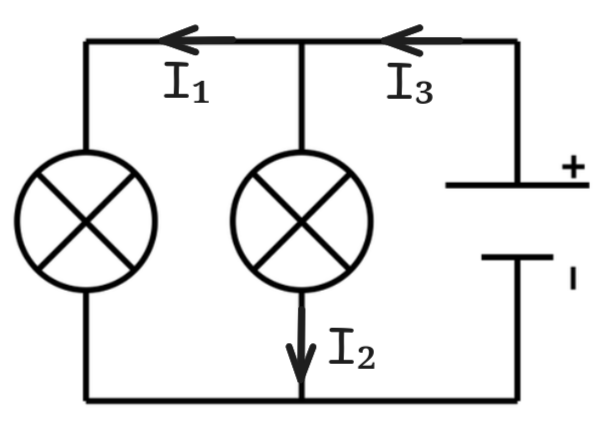
En justifiant à l'aide d'une loi et d'un calcul, donner la valeur de l'intensité I₁.
On est dans un circuit en dérivation on utilise donc la loi d'additivité des intensités : l'intensité de la branche principale (I) est égale à l'addition des autres intensités. On a donc : \(I_3 = I_1 + I_2\).
Soit : \(550 = I_1 + 250\) donc \(I_1 = 550 - 250 = 300 mA\).
Bonus : Si l'intensité \(I_1\) vaut 1,0 A et l'intensité I₂ vaut 550 mA, combien vaudrait l'intensité \(I_3\) ?
On applique la même loi avec 550 mA = 0,55 A. Donc : \(I_3=1,0 + 0,55 = 1,55A\).